about me¶
- applied econometrics, computer science (Master)
- economic theory (PhD)
- software for statistics and economtrics
- user-developer with various packages and with GAUSS, Matlab, Python
- scipy.stats
- statsmodels
- "self-taught statistician"
about statsmodels¶
- precursor: scipy.stats.models
- 7 years of development
- started with GSOC Skipper Seabold
- slow and steady growth since then
- GSOC Chad Fulton statespace models
- open source, BSD licensed
- ~ 130,000 LOC of Python (including some Cython)
Brief Overview - Time Series Analysis in Statsmodels¶
- Data Handling through Pandas
- statistics
- acf, pacf
- filters, seasonal decomposition
- hypothesis tests: unit root, Granger causality
- ARMA, ARIMAX
- VAR (vector autoregressive models)
- new statespace models
- SARIMAX
- ...
- postestimation: predict, impulse response, hypothesis testing
two GSOC projects in 2016 for TSA
%matplotlib inline
import datetime
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from dateutil.relativedelta import relativedelta
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tsa.stattools import acf
from statsmodels.tsa.stattools import pacf
from statsmodels.tsa.seasonal import seasonal_decompose
#plt.interactive(False) # otherwise interactive(False)
El Nino temperature data¶
from statsmodels.datasets.elnino import load_pandas
datadf = load_pandas()
datadf.data
temperature = np.asarray(datadf.data.iloc[:, 1:]).ravel()
nobs = len(temperature)
index = pd.date_range("1950-01-01", periods=nobs, freq='MS')
months = np.tile(np.arange(12), nobs // 12)
df_el = pd.DataFrame({'temperature': temperature, 'month': months}, index=index)
df_el.tail()
| month | temperature | |
|---|---|---|
| 2010-08-01 | 7 | 19.49 |
| 2010-09-01 | 8 | 19.28 |
| 2010-10-01 | 9 | 19.73 |
| 2010-11-01 | 10 | 20.44 |
| 2010-12-01 | 11 | 22.07 |
ax = df_el['temperature'].plot()
ax.figure.set_size_inches(12, 8)
ax.set_title('Temperature', fontsize=18)
<matplotlib.text.Text at 0xb0a39b0>
ax = df_el['temperature'].iloc[-12*5:].plot(style='-o')
ax.figure.set_size_inches(12, 8)
_ = ax.set_title('Temperature', fontsize=18)
res_ols = sm.formula.ols('temperature ~ C(month)', df_el.iloc[:-3*12]).fit()
predicted = res_ols.predict(df_el.iloc[-3*12:])
fitted = res_ols.fittedvalues.loc['2005-12-01':] # 5 years
ax = df_el['temperature'].iloc[-12*5:].plot(style='-o')
ax.figure.set_size_inches(12, 6)
fitted.plot(lw=2, color='r')
predicted.plot(lw=2, color='r')
ax.vlines(predicted.index[0], lw=4, alpha=0.25, *ax.get_ylim())
_ = ax.set_title('Constant Seasonal Pattern - fitted and predicted', fontsize=18)
ax = res_ols.resid.iloc[-5*12:].plot(style='-o',figsize=(12,8))
_ = ax.set_title('Residuals insample', fontsize=18)
_ = cfplot(res_ols.resid, lags=36)
import patsy
y, x = patsy.dmatrices('temperature ~ C(month)', df_el, return_type='dataframe')
res_arma = sm.tsa.ARMA(y, order=(2, 1), exog=x.iloc[:, 1:]).fit()
print(res_arma.summary())
ARMA Model Results
==============================================================================
Dep. Variable: temperature No. Observations: 732
Model: ARMA(2, 1) Log Likelihood -414.032
Method: css-mle S.D. of innovations 0.425
Date: Thu, 02 Jun 2016 AIC 860.064
Time: 15:24:59 BIC 933.597
Sample: 01-01-1950 HQIC 888.430
- 12-01-2010
=====================================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------------
const 24.3818 0.156 156.691 0.000 24.077 24.687
C(month)[T.1] 1.4486 0.055 26.240 0.000 1.340 1.557
C(month)[T.2] 1.8576 0.082 22.683 0.000 1.697 2.018
C(month)[T.3] 0.9966 0.100 9.948 0.000 0.800 1.193
C(month)[T.4] -0.2283 0.112 -2.034 0.042 -0.448 -0.008
C(month)[T.5] -1.5569 0.119 -13.076 0.000 -1.790 -1.324
C(month)[T.6] -2.6479 0.121 -21.827 0.000 -2.886 -2.410
C(month)[T.7] -3.5504 0.119 -29.805 0.000 -3.784 -3.317
C(month)[T.8] -3.8111 0.112 -33.934 0.000 -4.031 -3.591
C(month)[T.9] -3.5347 0.100 -35.229 0.000 -3.731 -3.338
C(month)[T.10] -2.8756 0.082 -35.012 0.000 -3.037 -2.715
C(month)[T.11] -1.7094 0.056 -30.741 0.000 -1.818 -1.600
ar.L1.temperature 1.3572 0.177 7.649 0.000 1.009 1.705
ar.L2.temperature -0.4388 0.161 -2.723 0.007 -0.755 -0.123
ma.L1.temperature -0.2634 0.193 -1.363 0.173 -0.642 0.115
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.2109 +0.0000j 1.2109 0.0000
AR.2 1.8819 +0.0000j 1.8819 0.0000
MA.1 3.7962 +0.0000j 3.7962 0.0000
-----------------------------------------------------------------------------
pred_dynamic = res_arma.predict(start='2008-12-01', end='2010-12-01', exog=res_arma.model.exog[-3*12:, 1:], dynamic=True)
fitted = res_arma.fittedvalues
Short term and long term forecasts¶
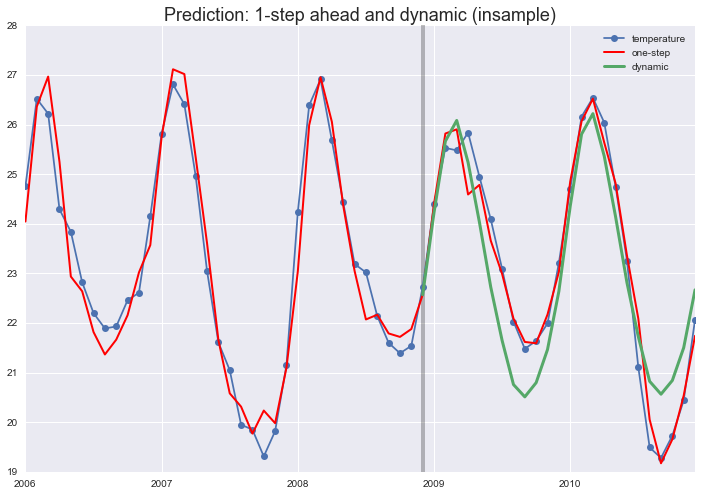
Summary ARMAX¶
y = X b + e, e ~ ARMA(p, q)¶
use explanatory variables X to model stable, systematic part¶
- seasonal patterns: dummies, splines, fourier polynomials
- trend: linear, polynomial, or piecewise
- other effects: dummies for special events, outliers
- explanatory variables: related series that help in prediction, (need forecasts for those, or use lagged values)
use ARMA to improve short term forecasting¶
- e = y - X b
- use the additional information that is left after systematic part has been removed
- assumes what is left over is stationary
Stationarity¶
A time series is stationary if the distribution of the observations does not depend on time.¶
Often only mean, variance and autocovariance stationarity is relevant
no persistence: shocks or disturbances have not long term effect
mean reversion: the long term forecast moves to the mean of the series
Random Walk y(t) = y(t-1) + e(t)¶
The best forecast at time t $\hat{y}(t+1) = y(t)$ and $\hat{y}(t+h) = y(t)$
Tomorrow is like today.
seasonal y(t) = y(t - s) + e(t)
Tomorrow is like the same day last week (month, year)
full persistence: every shock stays forever¶
y(t) is integrated, the differenced series is stationary
substituting back in
$y(t) = y(0) + \sum_{i=1}^{t} e(t-i)$
SARIMAX without X¶
SARIMAX(endog, exog=None, order=(1, 0, 0), seasonal_order=(0, 0, 0, 0), trend=None, ...)¶
endog is endogenous, dependent variable (statsmodels econometrics history)
exog are eXogenous, independent, explanatory variables
order (p, d, q) is regular ARIMA
seasonal_order (P, D, Q, s) is seasonal ARIMA with season length s
example: SARIMA((1, 0, 0), (1, 0, 0, 12) only AR terms
$(1 - a_1 \hspace{2mm} L) (1 - A_1 \hspace{2mm} L^{12}) y_t = y_t - a_1 \hspace{2mm} y_{t-1} - A_1 \hspace{2mm} y_{t-12} + a_1 \hspace{2mm} A_1 \hspace{2mm} y_{t-13}$¶
$y_t = a_1 \hspace{2mm} y_{t-1} + A_1 \hspace{2mm} y_{t-12} - a_1 \hspace{2mm} A_1 \hspace{2mm} y_{t-13} \hspace{2mm} + ...$¶
Model Selection and Automatic Forecasting¶
Hyndman has several supporting functions in R, auto.arima
statsmodels doesn't have much ready made and automatic
Amount of Differencing¶
(standard maximum likelihood methods do not apply)
commonly based on unit root or stationarity tests
Lag lengths, p, q, P, Q¶
loop over set of lag lengths and choose the model
minimize AIC, BIC, or maximize out-of-sample forecast performance.
Outliers, ...¶
dummies for outlier observation, trend breaks, ...
Example: Forecasting Bus Riders¶
see blog post and notebook for details
http://www.seanabu.com/2016/03/22/time-series-seasonal-ARIMA-model-in-python/
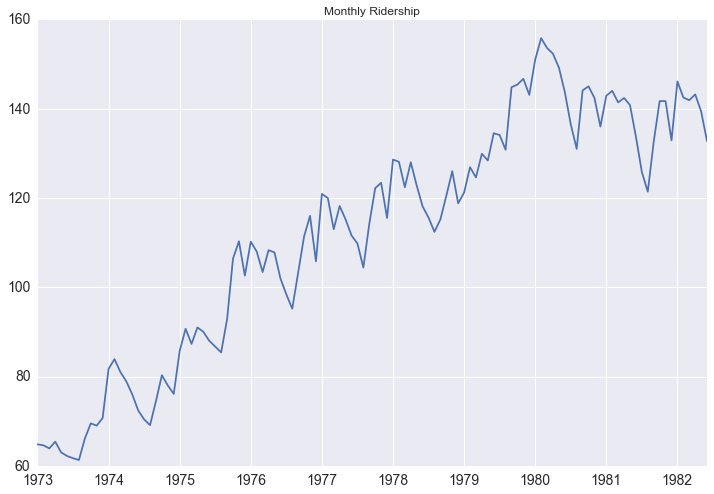
seas = seasonal_decompose(df['riders'])
fig = seas.plot()
fig.set_size_inches(12,8)
mod = sm.tsa.statespace.SARIMAX(df.riders, order=(0,1,0), seasonal_order=(1,1,1,12), trend='n')
results = mod.fit()
results.summary()
| Dep. Variable: | riders | No. Observations: | 114 |
|---|---|---|---|
| Model: | SARIMAX(0, 1, 0)x(1, 1, 1, 12) | Log Likelihood | -268.775 |
| Date: | Thu, 02 Jun 2016 | AIC | 543.550 |
| Time: | 15:25:04 | BIC | 551.759 |
| Sample: | 01-01-1973 | HQIC | 546.881 |
| - 06-01-1982 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| ar.S.L12 | 0.3235 | 0.186 | 1.737 | 0.082 | -0.042 | 0.688 |
| ma.S.L12 | -0.9989 | 39.033 | -0.026 | 0.980 | -77.502 | 75.504 |
| sigma2 | 9.8489 | 383.190 | 0.026 | 0.979 | -741.190 | 760.888 |
| Ljung-Box (Q): | 36.55 | Jarque-Bera (JB): | 4.81 |
|---|---|---|---|
| Prob(Q): | 0.63 | Prob(JB): | 0.09 |
| Heteroskedasticity (H): | 1.48 | Skew: | 0.38 |
| Prob(H) (two-sided): | 0.26 | Kurtosis: | 3.75 |
df['forecastd'] = results.predict(start=102, end=114, dynamic=True)
df['forecastnd'] = results.predict(start=102, end=114, dynamic=False)
df[['riders', 'forecastd', 'forecastnd']].loc['1979-01-01':].plot(figsize=(12, 8), color='brk', lw=3, alpha=0.5)
plt.savefig('images/ts_df_predict.png', bbox_inches='tight')
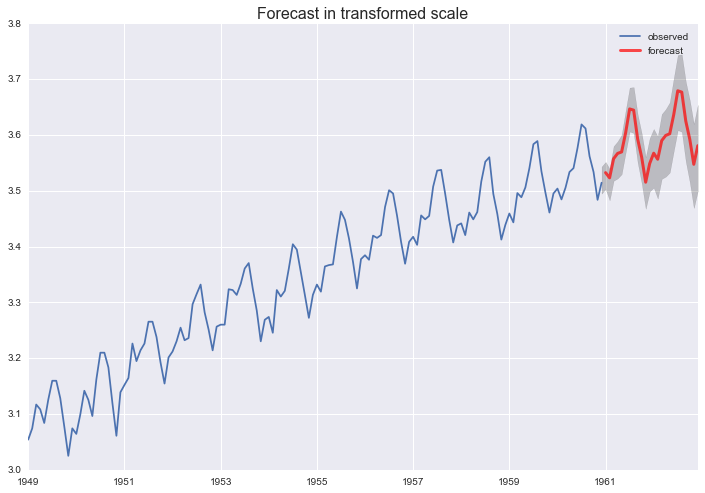
SARIMAX and transformation¶
back to the initial plot
df_air = pd.read_csv('AirPassengers.csv', index_col=0)
di = pd.date_range("1949-01-01", periods=144, freq='MS')
df_air.set_index(di, inplace=True)
del df_air['time']
df_air.tail()
| AirPassengers | |
|---|---|
| 1960-08-01 | 606 |
| 1960-09-01 | 508 |
| 1960-10-01 | 461 |
| 1960-11-01 | 390 |
| 1960-12-01 | 432 |
df_air.plot(figsize=(12,6))
plt.savefig('air_passenger.png', bbox_inches='tight')
air_log = np.log(df_air['AirPassengers'])
air_log.plot(figsize=(12,6))
<matplotlib.axes._subplots.AxesSubplot at 0xda44b70>
Rolling Standard Deviation - orginal versus log transformed¶
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(12,6))
_ = df_air['AirPassengers'].rolling(12).std().plot(ax=ax1)
_ = air_log.rolling(12).std().plot(ax=ax2)
Rolling Standard Deviation - Box-Cox transformed¶
from scipy import special
ax = special.boxcox(df_air['AirPassengers'], -0.2).rolling(window=12).std().plot(figsize=(12,6))
def box_cox_rolling_coeffvar(box_cox_param, endog, freq):
"""helper to find Box-Cox transformation with constant standard deviation
returns RLM results instance
"""
roll_air = special.boxcox(endog, box_cox_param).rolling(window=freq)
y = roll_air.std()
m = roll_air.mean()
x = sm.add_constant(m)
res_rlm = sm.RLM(y, x, missing='drop').fit()
return res_rlm
endog = df_air['AirPassengers']
freq = 12
tt = [(lam, box_cox_rolling_coeffvar(lam, endog, freq).pvalues[1]) for lam in np.linspace(-1, 1, 21)]
tt = np.asarray(tt)
print(tt[tt[:,1].argmax()])
[-0.2 0.62121147]
SARIMAX((1, 1, 1), (0, 1, 1, 12)) of transformed series¶
air_t = special.boxcox(df_air['AirPassengers'], -0.2)
res_s = sm.tsa.SARIMAX(air_t, order=(1, 1, 1), seasonal_order=(0, 1, 1, 12)).fit()
res_s.summary().tables[1]
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| ar.L1 | 0.1996 | 0.177 | 1.127 | 0.260 | -0.147 | 0.547 |
| ma.L1 | -0.5999 | 0.154 | -3.897 | 0.000 | -0.902 | -0.298 |
| ma.S.L12 | -0.6009 | 0.100 | -6.018 | 0.000 | -0.797 | -0.405 |
| sigma2 | 0.0002 | 1.67e-05 | 9.120 | 0.000 | 0.000 | 0.000 |
max_ar, max_ma = 3, 3
aic_full = pd.DataFrame(np.zeros((max_ar, max_ma), dtype=float))
# Iterate over all ARMA(p,q) models with p,q in [0,1, 2]
for p in range(max_ar):
for q in range(max_ma):
if p == 0 and q == 0:
continue
# Estimate the model with no missing datapoints
mod = sm.tsa.statespace.SARIMAX(air_t, order=(p,1,q), seasonal_order=(0, 1, 1, 12), trend='c', enforce_invertibility=False)
try:
res = mod.fit()
aic_full.iloc[p,q] = res.aic
except:
aic_full.iloc[p,q] = np.nan
print('min at ', np.asarray(aic_full).argmin())
aic_full
m:\josef_new\eclipse_ws\statsmodels\statsmodels_py34_pr\statsmodels\base\model.py:472: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning)
min at 7
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0.000000 | -764.890953 | -763.534483 |
| 1 | -761.633653 | -760.546620 | -761.033586 |
| 2 | -760.518611 | NaN | -760.842710 |
pred = res_s.get_prediction(start='1960-12-01', end='1962-12-01')
pred_ci = pred.conf_int()
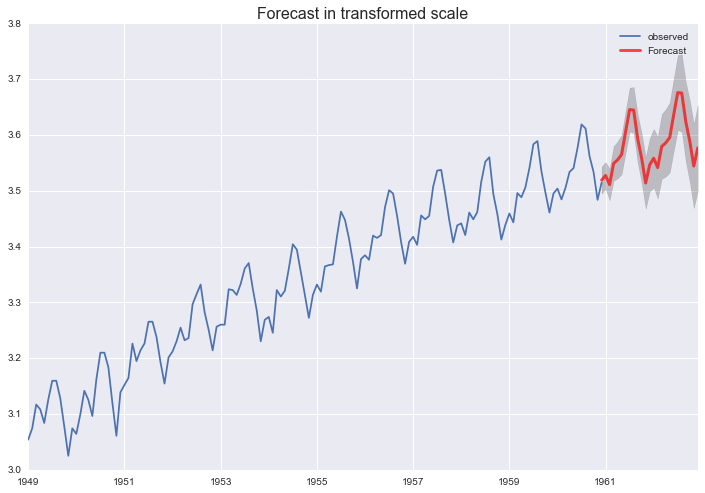
Transform forecast to original scale¶
pred_ci_orig = special.inv_boxcox(pred.conf_int(), -0.2)
forecast = special.inv_boxcox(pred.predicted_mean, -0.2)
ax = df_air['AirPassengers'].plot(label='observed')
ax.figure.set_size_inches(12, 8)
forecast.plot(ax=ax, label='forecast', lw=3, alpha=.7, color='r')
ax.fill_between(pred_ci_orig.index,
pred_ci_orig.iloc[:, 0],
pred_ci_orig.iloc[:, 1], color='k', alpha=.15)
ax.set_title('Forecast in original units (Median)', fontsize=16)
plt.legend()
plt.savefig('images/airpassenger_forecast.png', bbox_inches='tight')
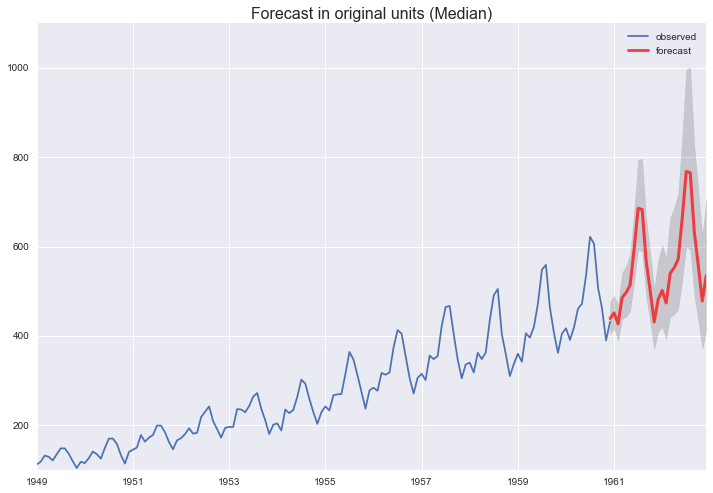
mod_ucarima = sm.tsa.UnobservedComponents(air_t, 'lltrend', seasonal=12, autoregressive=4)
res_ucarima = mod_ucarima.fit(method='powell', disp=0)
print(res_ucarima.summary())
Unobserved Components Results
=====================================================================================
Dep. Variable: AirPassengers No. Observations: 144
Model: local linear trend Log Likelihood 383.095
+ stochastic seasonal(12) AIC -748.190
+ AR(4) BIC -721.462
Date: Thu, 02 Jun 2016 HQIC -737.329
Time: 15:25:16
Sample: 01-01-1949
- 12-01-1960
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 3.632e-06 2.36e-05 0.154 0.877 -4.25e-05 4.98e-05
sigma2.level 3.352e-06 0.000 0.029 0.977 -0.000 0.000
sigma2.trend 1.663e-08 5.55e-08 0.299 0.765 -9.22e-08 1.25e-07
sigma2.seasonal 8.668e-06 5.05e-06 1.718 0.086 -1.22e-06 1.86e-05
sigma2.ar 7.536e-05 0.000 0.535 0.593 -0.000 0.000
ar.L1 0.8109 0.397 2.044 0.041 0.033 1.588
ar.L2 0.1013 0.179 0.566 0.571 -0.249 0.452
ar.L3 -0.2952 0.510 -0.579 0.562 -1.294 0.704
ar.L4 0.2732 0.338 0.807 0.419 -0.390 0.936
===================================================================================
Ljung-Box (Q): 46.20 Jarque-Bera (JB): 4.62
Prob(Q): 0.23 Prob(JB): 0.10
Heteroskedasticity (H): 0.56 Skew: -0.13
Prob(H) (two-sided): 0.06 Kurtosis: 3.88
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
fig_uc = res_ucarima.plot_components()
fig_uc.set_size_inches(12, 8)
pred_uc = res_ucarima.get_forecast(steps=24)
pred_ci = pred.conf_int()
#pred_uc.predicted_mean
References¶
documentation¶
http://www.statsmodels.org/dev/tsa.html
http://www.statsmodels.org/dev/statespace.html
http://www.statsmodels.org/dev/examples/index.html
blog posts¶
http://tomaugspurger.github.io/modern-7-timeseries.html Pandas usage
http://www.seanabu.com/2016/03/22/time-series-seasonal-ARIMA-model-in-python/
http://www.analyticsvidhya.com/blog/2016/02/time-series-forecasting-codes-python/
I will clean up notebook during weekend